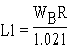|
Loudspeaker Diffraction Loss
|
||||
|
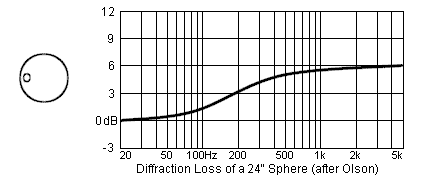
Loudspeaker enclosure "diffraction loss" occurs in the low frequency range of loudspeakers in enclosures that are located in the open, away from walls or other surfaces. The essence of it is this: At high frequencies the speaker is radiating into "half space" i.e. it is only radiating into the forward hemisphere. No significant energy is radiated to the rear of the speaker. At low frequencies the speaker is radiating into both the forward hemisphere and the rear hemisphere. That is, at low frequencies the speaker radiates into "full space". Because the "energy density" at low frequencies is reduced there is a loss of bass. In short, speaker systems designed for radiation into half space (mounted flush on an infinite plane) exhibit a loss of bass when implemented in typical speaker enclosures. Fortunately, this bass loss can be accurately modeled and subsequently compensated. Most loudspeaker modeling is performed based on the assumption of radiation into half space. A speaker radiating into half space plays 6 dB louder than the same speaker radiating into full space. This is the crux of the diffraction loss. A full range speaker finds itself radiating into half space at the upper frequencies but radiating into full space at lower frequencies. As a result, there is a gradual shift of -6dB from the highs to the lows. This is what is called the "6 dB baffle step" or the enclosure’s "diffraction loss". The center frequency of the transition is dependent on the dimensions of the baffle. The smaller the baffle the higher the transition frequency. The shape of the diffraction loss frequency response curve depends on the size and shape of the enclosure. Olson has carefully documented the diffraction loss of enclosures of various shapes (see references below). All enclosure shapes exhibit a basic 6 dB transition (or "step") in the response with the bass ending up 6 dB below the treble. A spherical enclosure exhibits this transition clearly with a very smooth diffraction loss curve. In the curves below I have taken the liberty of extending the frequency range of Olson's original graphs from 100 Hz to 20 Hz at the low end and from 4kHz to 5 kHz at the high end. The low frequency response was extended to more clearly reveal the "stepped" nature of the response. I wanted it to be clear that the response levels off at the low end. Olson's own reproductions of the measured diffraction loss of a sphere by Muller, Black, and Davis tend to confirm that my extensions to the responses are correct.
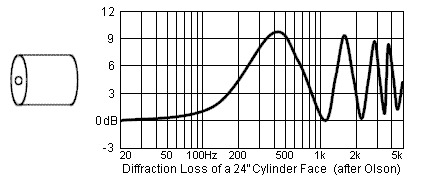
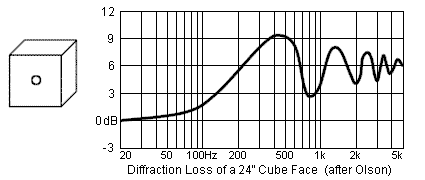
More "angular" enclosures exhibit the underlying 6 dB step along with a series of response ripples that are dependent on the placement of the speaker with respect to the baffle edges. The worst case appears to be placing the driver at the center of a circular baffle so that it is the same distance from all diffracting edges.
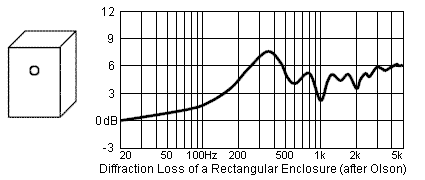
Placing the driver on the baffle so that it is a different distance from each edge tends to minimize the response ripples and make the diffraction loss look more like the smooth loss of the sphere. Olson's rectangular enclosure is an improvement over the cube and the cylinder face but the driver is still equidistant from three edges. Other authors report further reduction in the ripples with careful driver placement and edge rounding.
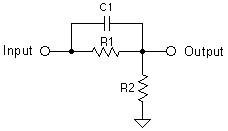
Because the spherical diffraction loss is a common element for the diffraction of all enclosures and the response ripples are much more difficult to predict (and can be minimized anyway) it makes sense to approximate the diffraction loss of a loudspeaker as the diffraction loss of the equivalent sphere. One simple electrical circuit which produces a 6 dB step reduction in the bass response is shown below.
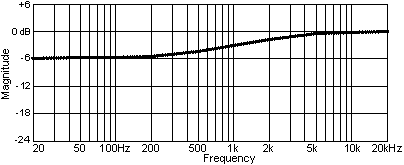
If we let R1 = R2 = R then a 6 dB attenuation results at low frequencies. At higher frequencies (where C1 becomes a low impedance) the attenuator is effectively bypassed and the signal is passed without attenuation. It can be shown that the 3 dB "center" frequency for the above network is given by:
The frequency response of diffraction modeling network typically looks like this:
Careful inspection of Olson's spherical diffraction loss curve reveals a -3dB frequency of about 190 Hz for the 24" sphere. Assuming that the 3 dB frequency is inversely proportional to the baffle diameter I have arrived at the following approximation for calculating the -3dB frequency as a function of baffle diameter.
f(3) = 115/W(B) or
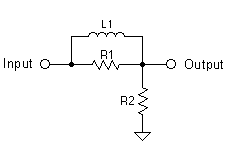
f(3) = 380/W(B) Sanity Check: for Olson's 24" (2 feet) baffle we calculate f(3) = 380/2 = 190 Hz . . .OK! Once the diffraction loss is known it is possible to design a simple electrical network that will exactly mirror the spherical diffraction loss and restore the lost bass to a speaker system. Loudspeaker designers have traditionally compensated for the diffraction loss by reducing the level of the tweeter and making other adjustments in the crossover. The method I propose is to design for half space but then do a precise mirror image compensation for the diffraction loss by way of an R-L network wired in series with the (impedance compensated) speaker. Alternately, the diffraction loss can be compensated at line level with a simple R-R-C network. Line level correction would reduce the requirement for the large inductors typically needed for a speaker level compensation network. A simple electrical network which produces a 6 dB step reduction in the treble response is shown below.
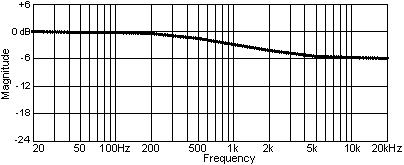
Here R2 represents the loudspeaker load impedance. If we let R1 = R2 = R then a 6 dB attenuation results at high frequencies. At lower frequencies (where L1 becomes a low impedance) the attenuator is effectively bypassed and the signal is passed to the driver (R2 here) without attenuation. The frequency response of 6 dB diffraction compensation network looks like this:
To design an RL network which will compensate for diffraction loss of a particular system we start by setting: R1 = R2 = R =Nominal System Impedance (8 Ohms for example) Next, you can use my empirically derived equation to calculate the value of the inductor L1:
Where W(B) is the baffle width in meters, R is in Ohms, and L1 in millihenrys. I arrived at this equation for L1 by forcing the 3 dB frequency of the compensating network to match the 3 dB frequency for the diffraction loss of the baffle. The resulting RL network should be wired in series with the speaker system it is compensating. The correction will be most accurate if the loudspeaker itself approximates a resistive load. Example: Find the network required to compensate the spherical diffraction loss of a 4 Ohm speaker system with a 0.25 meter wide baffle. R
= 4 (the
nominal impedance of the system) L1 = .25 x 4 / 1.021 = 1 / 1.021
L1 = .979 mH
To build this network, start by connecting a 4 Ohm resistor in parallel with a 1 mH inductor. Then connect this RL network in series with the speaker. You should hear reduced treble when the diffraction loss compensator is used. WinSpeakerz models the diffraction loss of the enclosure as a simple spherical diffraction loss. Provided the driver is located "irregularly" on the baffle this gives very good approximation to the actual diffraction loss of the enclosure. The frequency of the transition is controlled by the "Baffle Width" parameter at the System Editor page 1. The response of the speaker can be viewed with or without the diffraction loss and the diffraction loss can also be viewed separately. jlm |
||||
|
25Jun99 A follow-up post on this topic: Question: >
I've been researching the idea of adding a baffle step compensation
circuit The 6 dB loss is correct for a speaker enclosure in free space. When the enclosure is placed in a room it will encounter various effects due to the room (reverb, standing waves, boundary effect, cavity effect . . .) Diffraction loss and room effects are independent and completely different effects. The diffraction loss is nicely predictable whereas the effects of the room are highly variable, not only from room to room but also with speaker placement and room furnishing. This typically means that each listening environment will be unique and will require unique compensation. I suggest the 6 dB diffraction loss correction as a correction for the diffraction loss alone. I don't suggest that it will neutralize all the effects due to a unique listening environment. Others suggest you "deal with diffraction" in the crossover, usually by just lowering the tweeter level a bit. In some situations 3 or 4 dB of diffraction loss correction may result in an overall response that is closer to neutral (flat). But the most correct way to compensate the room would be to do it separately from any diffraction loss correction. Room compensation might take the form of several notch filters tuned to the worst peaks resulting from room modes. Next you might want to tilt the treble up a smidge to compensate for reverberation that has significant treble loss. Dark room reverb will make the playback sound a little darker. Bright reverb . . . bright. Next, depending on the size of the room and speaker response, you might need to compensate for the cavity effect. In larger rooms cavity effect can be ignored but in vehicle cabins it is a major effect. Diffraction loss compensation is only part of the job of precisely compensating for the difference between a theoretical half-space acoustic load and what happens when we place an enclosure in a real world listening room. Reducing the degree of diffraction loss compensation MAY reduce the coloration from the room effects as these effects largely tend to "boost the bass" but such an adjustment is imprecise at best. If we can systematically identify each source of color between our half space model and our particular listening room then we can then take steps to precisely neutralize the response in our own listening room. Spherical diffraction compensation is one effect we can correct with a high degree of precision. As we move toward a better understanding and modeling of our listening rooms I'm sure we will work out more practical and precise ways to compensate our rooms. Comments and critique are welcome. :-) Regards, John |