 ( Info & pics courtesy of T Cox & Peter D`Antonio
RPG acoustics)
( Info & pics courtesy of T Cox & Peter D`Antonio
RPG acoustics)
The sound that we hear in a room
is a combination of the direct sound and the indirect reflections from
the room's boundary surfaces and contents. Hence, one of the central
topics in room acoustics is how to manipulate these indirect reflections
that affect the way we perceive sound.
Sound striking a surface is either transmitted or reflected. The
reflected sound can either be attenuated by a sound absorbing surface,
re-directed by a reflecting surface or scattered by a diffusing surface.
When a significant portion of the reflected sound is uniformly
dispersed, we call the surface a diffusor. The past 100 years, since the
founding of architectural acoustics by Sabine, have largely been devoted
to studying how absorption affects sound. Over this time a library of
absorption coefficients have been tabulated based on accepted standards
and a reasonable understanding of how absorption should be applied in
room designs has been achieved.
By contrast, scientific knowledge on the role of diffusing surfaces has
only been developed much more recently. Over the past 20 years
significant research on methods to design, predict, measure, and
quantify sound diffusing surfaces by RPG has resulted in a
growing body of
information on this
topic. For example, RPG is working with international standards
organizations in an attempt to quantify the diffusivity, or the degree
to which a surface uniformly scatters incident sound, and the random
incidence scattering coefficient.
To provide a fast and accurate measurement of the directional scattering
properties of architectural surfaces, RPG research developed the first
2-dimensional 1:5 scale, high angular resolution, fixed multi-microphone
polar boundary measurement system using a maximum-length sequence (MLS)
fast Hadamard approach, which offers 70 dB of dynamic range. The
measurement hardware is based on the TEF-20 DSP, which samples at 48
kHz.

Figure 1 shows a sample at the center of two concentric semicircles. The
inner semicircle has a radius of 1m and contains 37 fixed Crown GLM-100
microphones providing 5 degree angular resolution. The outer semicircle
has a radius of 2m and contains fixed positions to vary the angle of
incidence of the loudspeaker.
Data Reduction
Measurement hardware
and computer control |
| Figure 2: Select image to enlarge 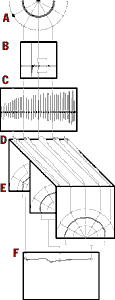 |
The data analysis is shown in Figure 2. To isolate the scattering from the sample under test (rectangle in B), a background measurement containing the direct sound and the room interference is subtracted. The speaker / microphone response is then deconvolved from the measurement and the scattered data are windowed. These windowed data for all of the angles of observation are concatenated in Figure 2C in the form of a "temporal" angular response. Each impulse response is transformed into its frequency response, Figure 2D, and 1/3 octave polar responses are obtained, Figure 2E. The auto correlation of these polar responses is used as a diffusion coefficient metric and is plotted versus frequency to obtain the diffusion response, Figure 2F.
3D Goniometer
For one dimensional scattering surfaces like cylinders and 1D QRDs, the 2D diffusion apparatus is useful. For two dimensional surfaces, a 3D goniometer is needed to measure the backscattering on the surface of a hemisphere. Such an apparatus has been designed and built as part of a grant funded by the Engineering Physical Sciences Research Council and RPG Diffusor Systems. This 3D goniometer is shown in Figure 3. The sample is placed at the center of the 1m radius microphone arc and the 2m speaker arc. For a given loudspeaker azimuth and elevation angle, measurements are made for various azimuth and elevation positions of the microphone to uniformly describe the performance on the surface of a hemisphere.

Figure 3